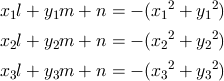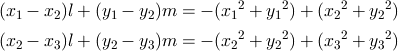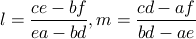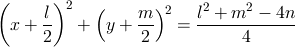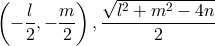Untitled Web Page

とある高専生の割と誰得なウェブページです。

Problem 0010:Circumscribed Circle of a Triangle

問題

Circumscribed Circle of a Triangle

平面上の点 (x1, y1)(x2, y2)(x3, y3) を頂点とした三角形の外接円の中心座標(xp, yp)と半径 r を出力して終了するプログラムを作成してください。x1, y1, x2, y2, x3, y3, xp, yp は、それぞれ -100 以上 100 以下とします。

Input

複数のデータセットが与えられます。最初にデータセット数 n が１行に与えられます。各データセットは以下の形式です。

x1 y1 x2 y2 x3 y3

ここで、各値は実数とします。

Output

各データセットに対して、xp, yp, r を１つのスペースで区切って１行に出力して下さい。小数点以下第３位まで出力して下さい。小数点第４位を四捨五入すること。

Sample Input

1
0.0 0.0 2.0 0.0 2.0 2.0

Output for the Sample Input

1.000 1.000 1.414

解法:三角形の外接円→三角形の各頂点を通る円

「三角形の外接円」が「三角形の各頂点を通る円」と同じということを twitter で教わるまで，「三角形の外接円」として(?)求めようとしていた自分。

円は x2 + y2 + lx + my + n = 0 という方程式で表される。x2 + y2 を右辺に移項すると，lx + my + n = − (x2 + y2) となる。これに三角形の 3 頂点 (x1, y1), (x2, y2), (x3, y3) を代入すると，次の 3 式ができる。

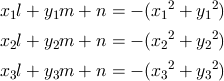
x_1l + y_1m + n = -({x_1}^2 + {y_1}^2) \\ x_2l + y_2m + n = -({x_2}^2 + {y_2}^2) \\ x_3l + y_3m + n = -({x_3}^2 + {y_3}^2)

さらに，(第 1 式) − (第 2 式)，(第 2 式) − (第 3 式) から以下の 2 式ができる。

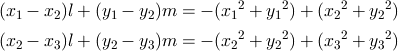
(x_1-x_2)l + (y_1-y_2)m = -({x_1}^2+{y_1}^2)+({x_2}^2+{y_2}^2) \\ (x_2-x_3)l + (y_2-y_3)m = -({x_2}^2+{y_2}^2)+({x_3}^2+{y_3}^2)

a = x1 − x2, b = y1 − y2, c = − (x12 + y12) + (x22 + y22), d = x2 − x3, e = y2 − y3, f = − (x22 + y22) + (x32 + y32) とおいて，上の 2 式を連立して解くと次のようになる。

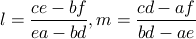
l = \frac{ce-bf}{ea-bd} , m = \frac{cd-af}{bd-ae}

そして，最初の第 1 式より n を求める。円の方程式 x2 + y2 + lx + my + n = 0 を変形すると次のようになる。

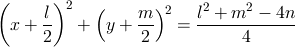
\left( x+\frac{l}{2} \right)^2 + \left( y+\frac{m}{2} \right)^2 = \frac{l^2+m^2-4n}{4}

よって出力する中心の座標と半径はそれぞれ以下のようになる。

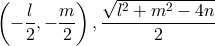
\left( -\frac{l}{2}, -\frac{m}{2} \right), \frac{\sqrt{l^2+m^2-4n}}{2}

小数点第４位を四捨五入し，小数点以下第３位まで出力する処理は <iomanip> のマニピュレータで行った。(数式画像の作成は数式画像作成ツールを用いた)

#include <iostream>
#include <iomanip>
#include <cmath>
struct {double x, y;} p[3];
using namespace std;
int main()
{
   int t, i, j;
   double r, a, b, c, d, e, f, l, m, n;
   cin >> t;
   for (i = 0; i < t; i++)
   {
      for (j = 0; j < 3; j++)
         cin >> p[j].x >> p[j].y;
      a = p[0].x-p[1].x;
      b = p[0].y-p[1].y;
      c = -(p[0].x*p[0].x)-(p[0].y*p[0].y)+(p[1].x*p[1].x)+(p[1].y*p[1].y);
      d = p[1].x-p[2].x;
      e = p[1].y-p[2].y;
      f = -(p[1].x*p[1].x)-(p[1].y*p[1].y)+(p[2].x*p[2].x)+(p[2].y*p[2].y);
      m = (c*d-a*f)/(b*d-a*e);
      l = (c*e-b*f)/(e*a-b*d);
      n = -((p[0].x*p[0].x)+(p[0].y*p[0].y)+p[0].x*l+p[0].y*m);
      cout << setprecision(3) << setiosflags(ios::fixed);
      cout << -l/2 << " " << -m/2 << " " << sqrt(l*l+m*m-4*n)/2 << endl;
   }
}